
今回からは「外力:重力」について説明していきます。
整形外科疾患の原点は、必ず「外力」です。
そして、外力は「アクシデント由来」「重力」「反力」の3つです。
その中でも特に、「重力」「反力」が運動器リハの最重要ポイントです。
つまり、ここからが最大の山場です。
力学のイメージをつかめると、あなたの臨床は大きく変化します。
今回の内容は、ぜひとも理解して頂きたいです。
それでは、始めましょう。

何度も申し上げている通り、「重力」「反力」が運動器リハのキーポイントです。
患者さんの症状と「重力」「反力」の関係を、しっかり考え抜いてください。
あなたの患者さんに共通する「痛みの根本原因」が、これらの外力です。
ところで、
「重力」「反力」が、からだへの負担となることをイメージできますか?
「何となくそんな気がする」では、臨床で使えません。
力学を臨床で使える武器にする。
そのためには、「力学の基礎知識」の確認が必要です。
では早速、力学の理解を深めていきましょう。
基礎知識とあなたの臨床が、しっかりと繋がるように解説します。
あなたが力学を苦手としていることは分かっています。
だから、「こんな基礎的なこと、もう分かってるでしょ?」みたいな解説はしません。
苦手で分からない。
嫌いで考えたくもない。
それを踏まえた上で解説していきます。
可能な限り、ついてきてください。
1つの四角形があります。
水平な地面の上に置かれています。
この1つを土台にして、積み木のように四角形を積み重ねていきます。
あなたは、図を見ながら「崩れそう」「崩れなさそう」を感じ取ってみて下さい。
奥行きは無視して、前額面だけで考えてみて下さい。
では、まずは1個、積んでみましょう。
さらにもう1個、上に乗せてみましょう。
合計3個になりました。
この3個ですが、崩れそうなイメージはありますか?
これで「崩れてしまいそう」と感じる人は、いないと思います。
では、これはどうでしょうか?
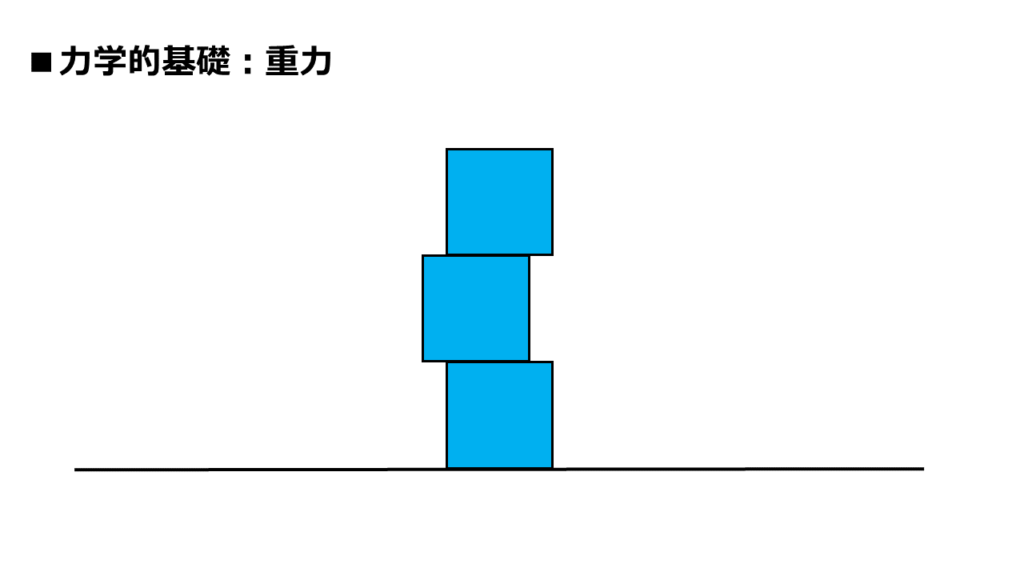
真ん中の1つが少しズレました。
とは言っても、これで「崩れそう」と感じる人は、まだいないと思います。
さらに4つ目を積もうとしても、気になるズレではないと思います。
では、これはどうでしょうか?
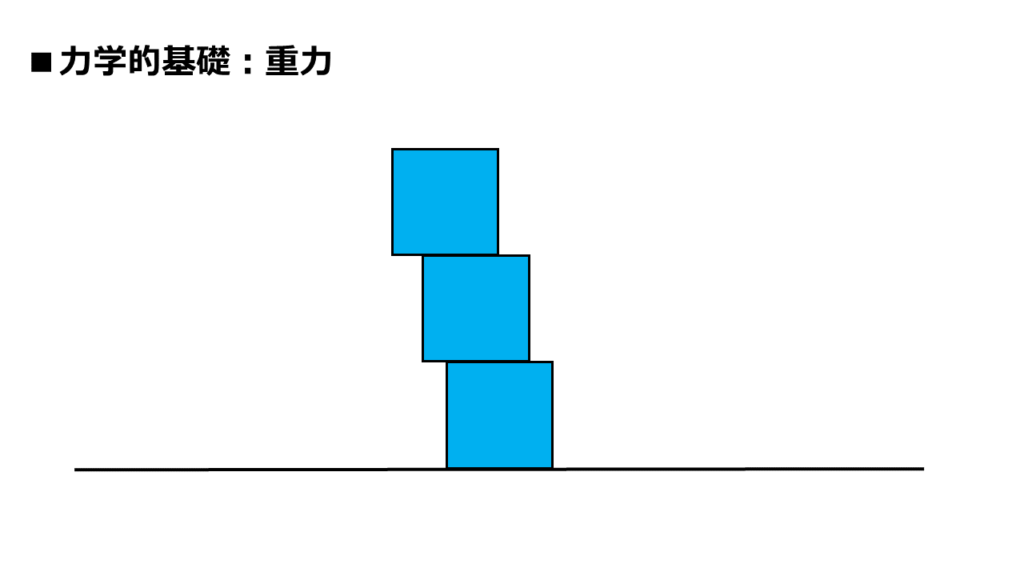
先ほどよりも「崩れそう」と感じませんか?
1つ前の図との違いは、「最上段の1個の位置だけ」です。
下2つの位置関係は変わっていません。
最上段の1つが、左側にズレただけです。
それだけの変化なのに、急に不安定さが増しませんか?
たった1つの位置関係が変わるだけで、印象はだいぶ変わります。
この上に4個目を置くとなると、先ほどよりも慎重になりそうです。
では、次の場合はどう感じますか?
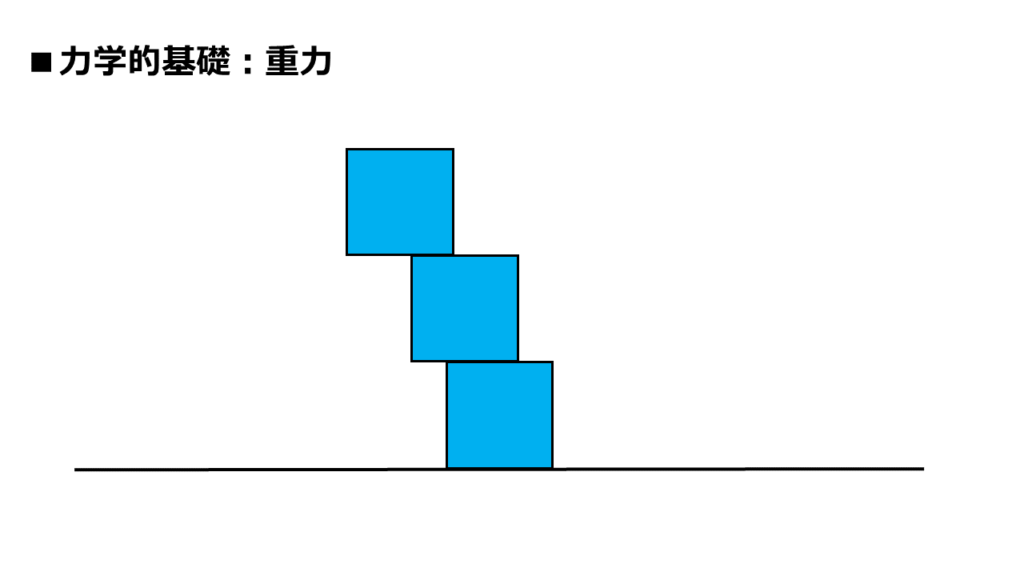
これは崩れそうですね。
最上段の四角形は、手を離したら、すぐに左側へ落ちそうです。
真ん中の四角形も、巻き添えとなりそうです。
さらに、これはどうでしょうか?
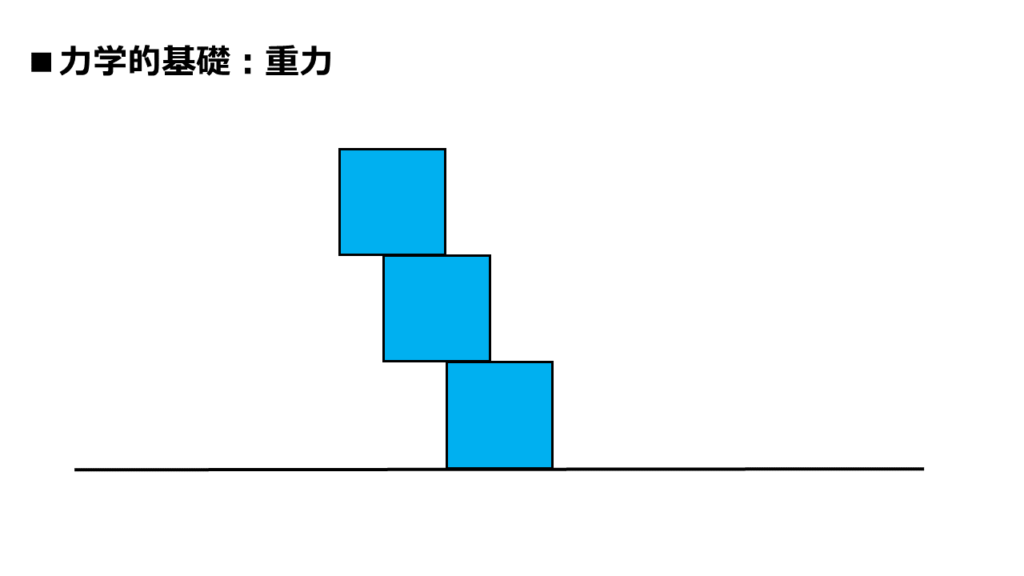
こうなると、そもそも、真ん中の四角形の段階で崩れそうに感じます。
では、この積み木の不安定さをイメージしたまま、次の例を見て下さい。
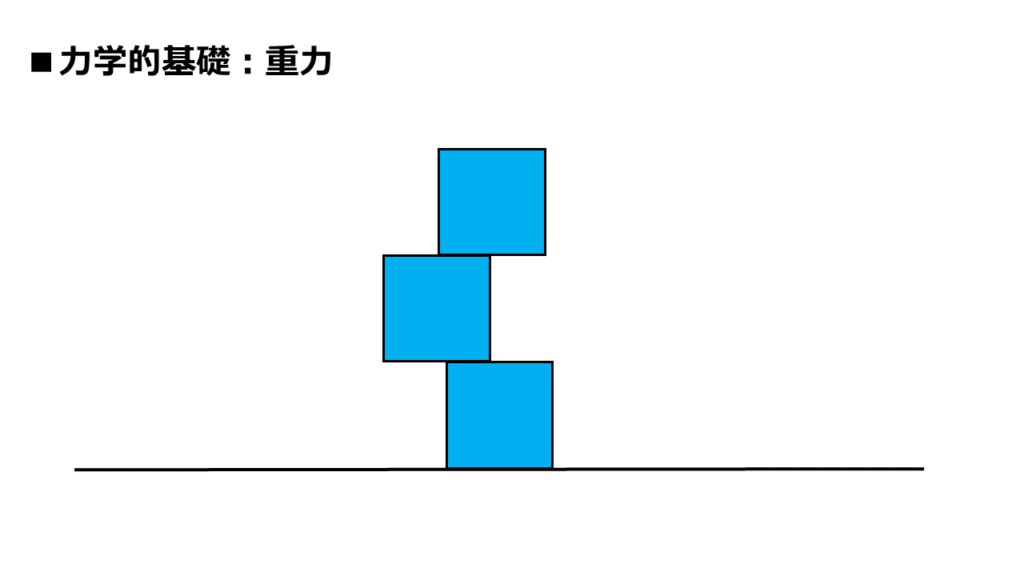
いかがでしょうか? 印象が変わりませんか?
前の図との違いは、最上段の四角形が右側に移動しただけです。
下2つの位置関係は、まったく変わっていません。
たったそれだけで、「崩れそう」だったのが「なんか大丈夫そう」に変わりませんか?
いくつか見比べてきましたが、四角形の位置関係によってイメージが変化しますね。
この感覚的な変化の理由を、言葉で説明できますか?
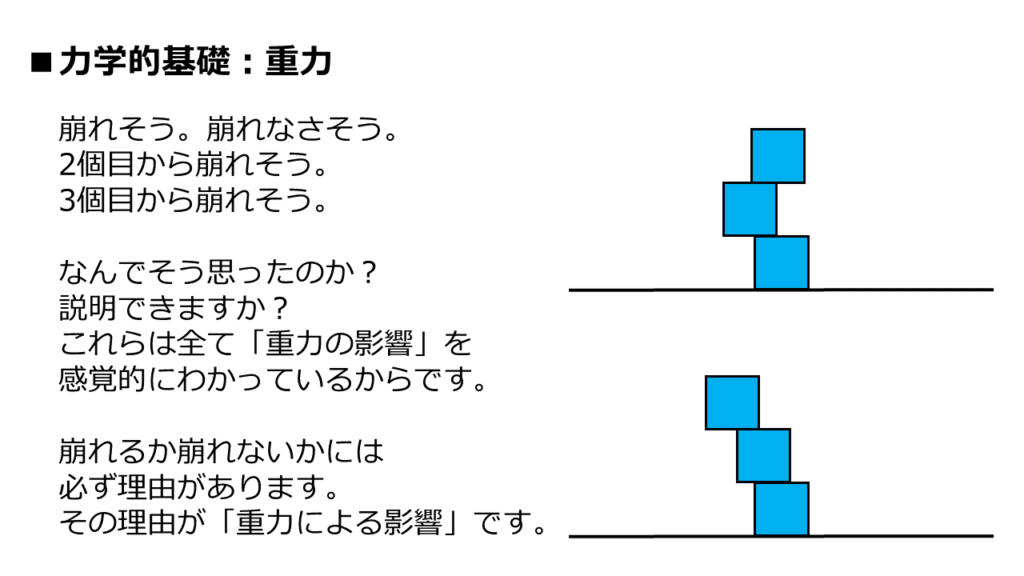
感覚的な変化の理由は「重力の影響」によるものです。
既にあなたは、日々の生活を通じて、「重力の影響」を感覚的に理解しています。
言葉や理屈で説明できなくても、感覚的に分かっているのです。
だから、「これは崩れそう」とか「これは崩れなさそう」とかを感じたわけです。
「重力の影響を物理的に考えましょう」と言うと、つい難しく考えてしまいがちです。
しかし、それは先入観です。
既に感覚的に分かっていることに理屈を当てはめれば、誰でも「重力の影響」を考えられます。
では、あなたが既に持っている感覚を「言語化」して、臨床で使える武器に変えましょう。
まず、言語化に必要な知識は「重心」です。
聞き慣れた言葉だと思いますが、理解が曖昧だと武器にはなりません。
重心について考えてみましょう。
重心とは何でしょうか?
学生時代の授業と同じような説明をするなら、次のスライドの通りです。

「重心」を辞書で調べると、こんな説明でした。
「身体重心」については、学生時代の定番書籍「基礎運動学」からの引用です。
この説明で、意味が分かりますか?
意味を調べたのに、さらに意味不明になる説明です。
この説明で理解できるのであれば、みんな苦労しません。
もっと簡単に話を進めていきましょう。

と言うわけで、雑にまとめます。
こんな感じで、指一本で支えられる延長線上に「重心」は存在すると思ってください。
臨床で大事なことはシンプルさです。
こんな程度の理解でも、臨床で活用していく上では十分です。
でも、少しだけ補足させて下さい。
重心は「ピンポイント」で存在します。
「ここからここまで全部重心」みたいな、幅や広がりはありません。
「点」のようなものです。
そして、その1点さえしっかりと支えれば、理論上は何でも支えることができます。
球体に限った話ではありません。
四角形でも三角形でも、
長方形でも台形でも、
名前の付けようのない変な形でも、全部同じです。
「点として存在する重心」の真下を支えれば、指一本で支えることが出来ます。
ひとまず、「重心は点である」という認識をして下さい。
では、積み木の例に戻ります。
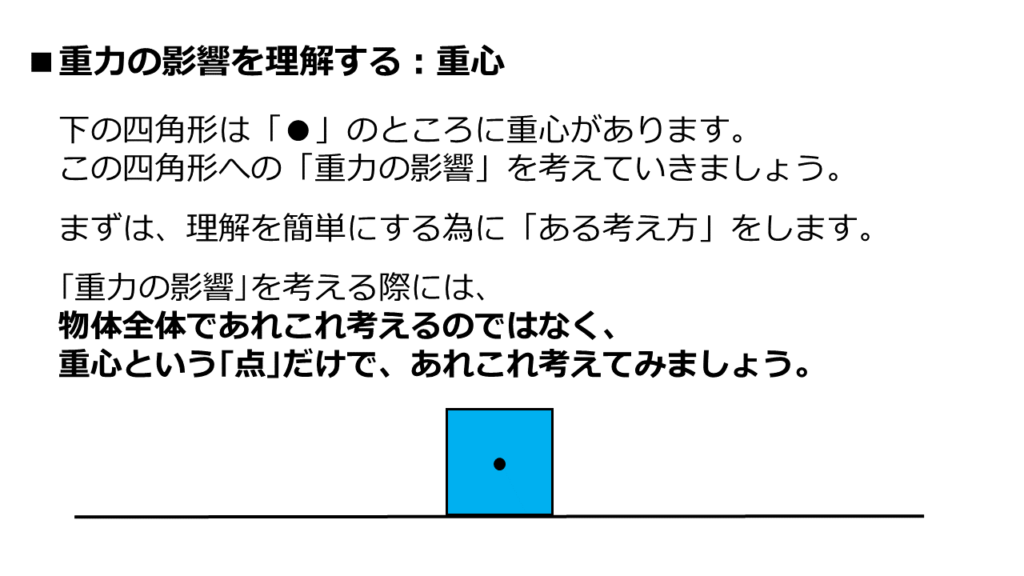
スライドの説明だけだと、よく分からないかもしれませんね。
具体的にどういうことなのかと言うと、以下のようなイメージです。
「重心が右へ行けば、四角形全体が右へ行きます」
「重心が下へ行けば、四角形全体が下へ行きます」
重心という「点」が動いた方向に向かって、物体全体は移動するということです。
当たり前に思うかもしれませんが、あえて意識的に、そのように考えてください。
では、説明を続けていきます。
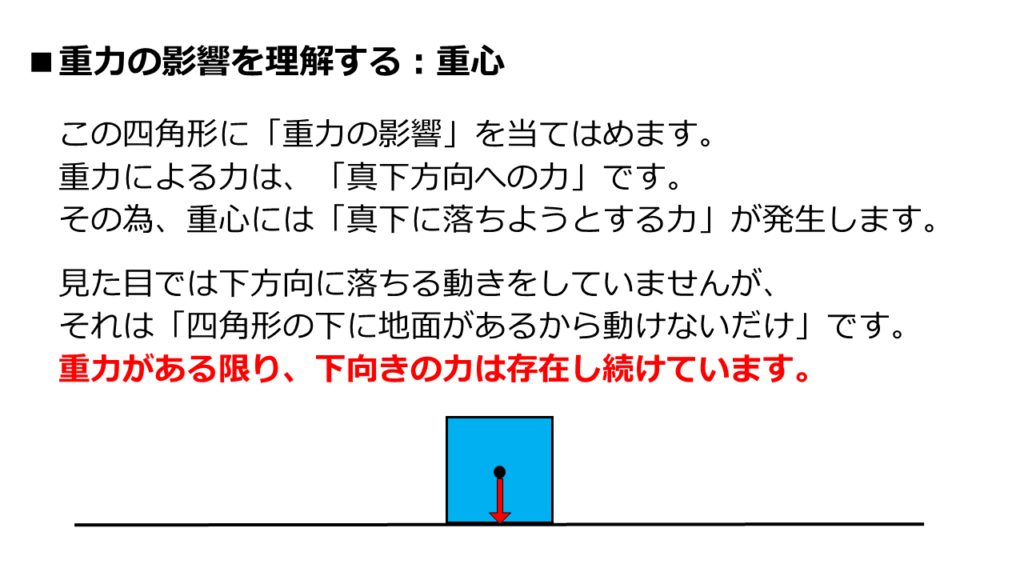
四角形への重力の影響を、赤い矢印で示しました。
重力による影響は、地球上どこでも「真下方向」です。
その為、この四角形は、重力の影響で真下に向かって落ちようとしています。
見た目には下方向に動いていませんが、地面があるから行けないだけです。
見た目の動きはなくても、いつでもずっと、下に落ちようとしています。
重力が存在する限り、このような「下向きの力」は、24時間365日存在し続けます。
ここで、先ほど紹介した考え方を当てはめます。
「物体全体で考えるのではなく、重心という1点だけで考える」という考え方です。
この考え方に基づいて「重力による影響」を書き込むと、赤矢印のような書き方になります。
重心という「1つの点」から矢印を書いて、この四角形の運動方向が示されました。
「重心が真下に行こうとしているから、四角形全体も真下に行こうとしている」となります。
もしも、重心を右へ動かす力が加わった場合は、重心から右方向に伸びる矢印を書きます。
その結果、四角形全体も右方向へ動くこととなります。
ひとまず、重心という「点」だけに注目して、物体全体の運動方向を考えましょう。
と、理屈をあれこれお伝えをしましたが、
現時点での最重要ポイントを明確にしておきます。
それは「重力の影響で、どんな物体も24時間365日、ずっと真下に落ち続けようとしている」です。
それでは、次のテーマに話を進めます。
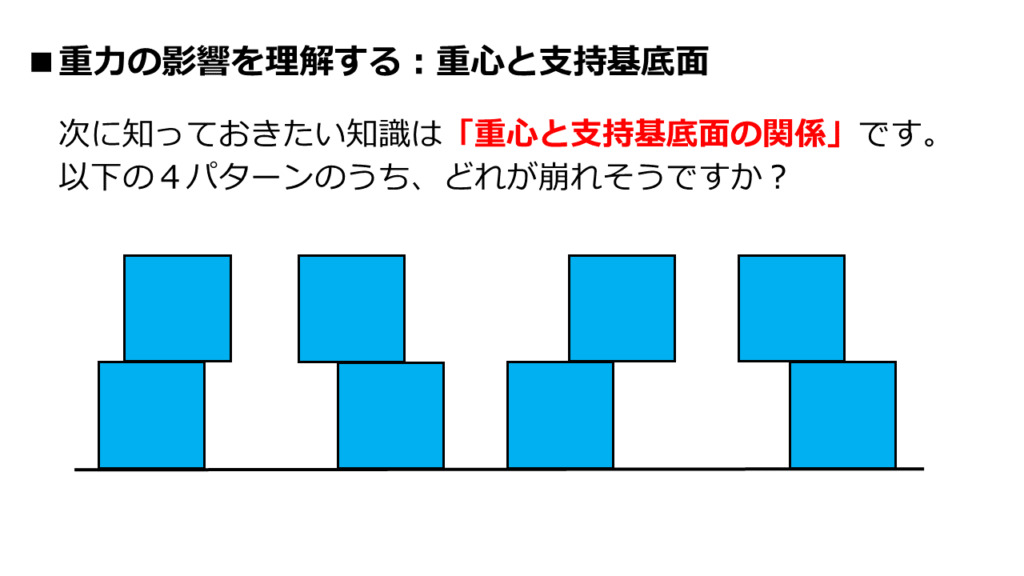
次のテーマは「重心と支持基底面の関係」です。
上の4パターンのうち、上側の四角形が落ちてしまいそうなのは、どの場合でしょうか?
見比べてみてください。
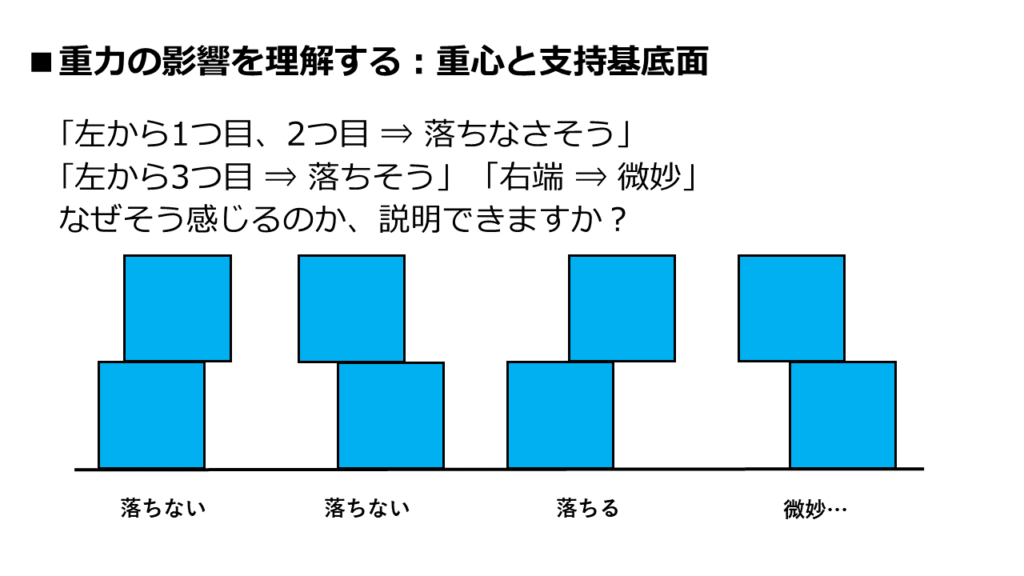
ほとんどの人が、同じ印象を持っていると思います。
感覚的にそう感じるのは、なぜでしょうか?
答えは「重心と支持基底面の関係」にあります。
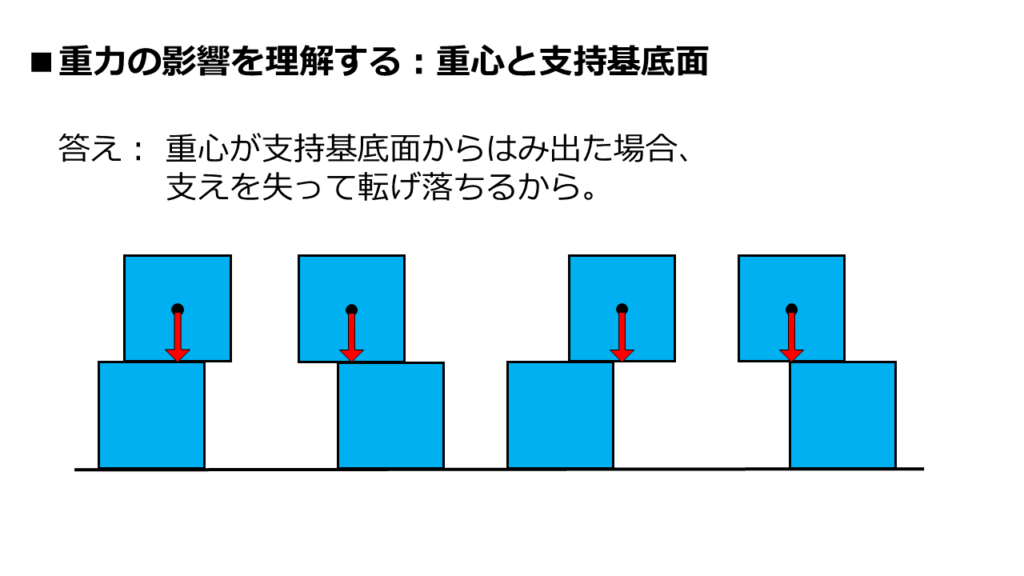
答えは簡単なことです。
上側の四角形の重心が、支持基底面からはみ出した場合に転げ落ちます。
この場合も、重心という「点」だけで、四角形全体の動きを考えます。
上側の四角形の重心は、重力の影響によって真下に行こうとしています。
その際、重心の真下に「支持基底面」があれば、重心が支えられて動くことはありません。
しかし、重心の真下に「支持基底面」が無ければ、重心は下方向に動いてしまいます。
つまり、重心の真下に支持基底面が無い場合、重心は真下へ移動をし始めます。
そして、重心が移動するということは、四角形全体も移動するということです。
その結果、四角形は下へ転落します。
図に示した左から1番目と2番目の四角形は、重心の真下に支持基底面があります。
だから、四角形は落下しません。
左から3番目は、重心の真下に支持基底面が存在しません。
重心は下へと移動することができてしまうので、四角形は落下します。
左から4番目は、支持基底面の端ギリギリのところに乗っかっています。
その為、理屈的には落ちません。
しかし、重心位置が少しでも左にズレれば、落ちてしまいます。
落ちそうにも見えるし、落ちなさそうにも見えるし…という感覚そのままです。
予想通りの結果でしたか?
予想通りなら、あなたは力学を分かっています。
力学と言うと難しい印象が付きまといます。
諦めたくなります。嫌いになります。
でも、あなたは既に、力学を感覚的に分かっています。
あなたが感覚的に分かっていることに、理屈をつけくわえるだけです。
難しいことを求めれば、話はどこまでも難しくできます。
しかし、臨床に必要最低限のレベルであれば、難しさは不要です。
あなたが感覚的に分かっている事に、ほんの少しだけ理屈をくっつけるだけです。
では、さらに話を進めます。
次のスライドへいきましょう。
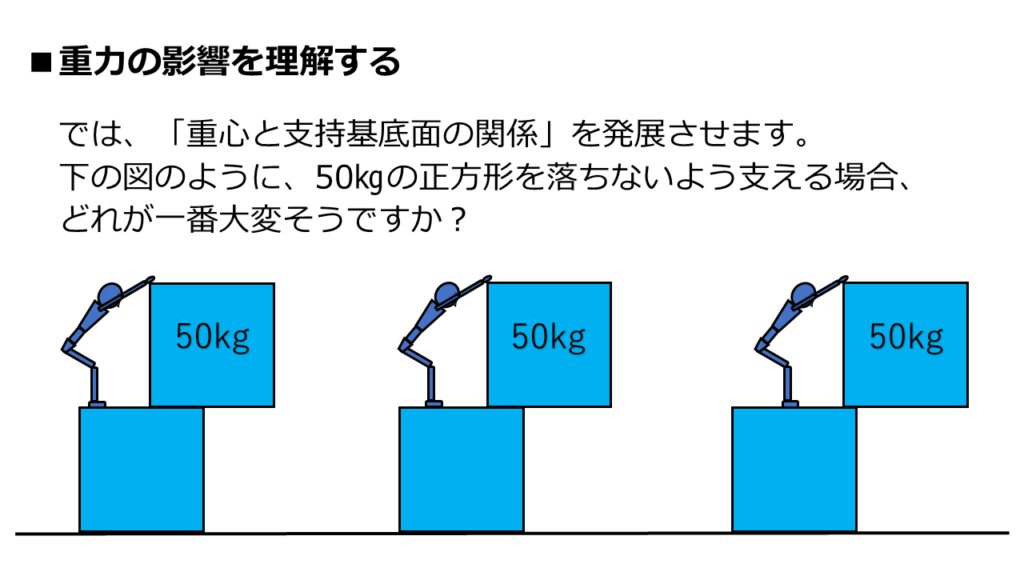
50㎏の重さの正方形を、落とさないように支えている人がいます。
この人は、正方形の端っこを上から押さえて、下に落とさないように頑張っています。
では、上の3パターンの内、どれが最も大変そうに見えますか?
50㎏という「重さ」は変わりません。
どれも同じ50㎏の正方形です。
唯一の違いは「正方形のズレ幅」だけです。
さて、どれが大変そうでしょうか?
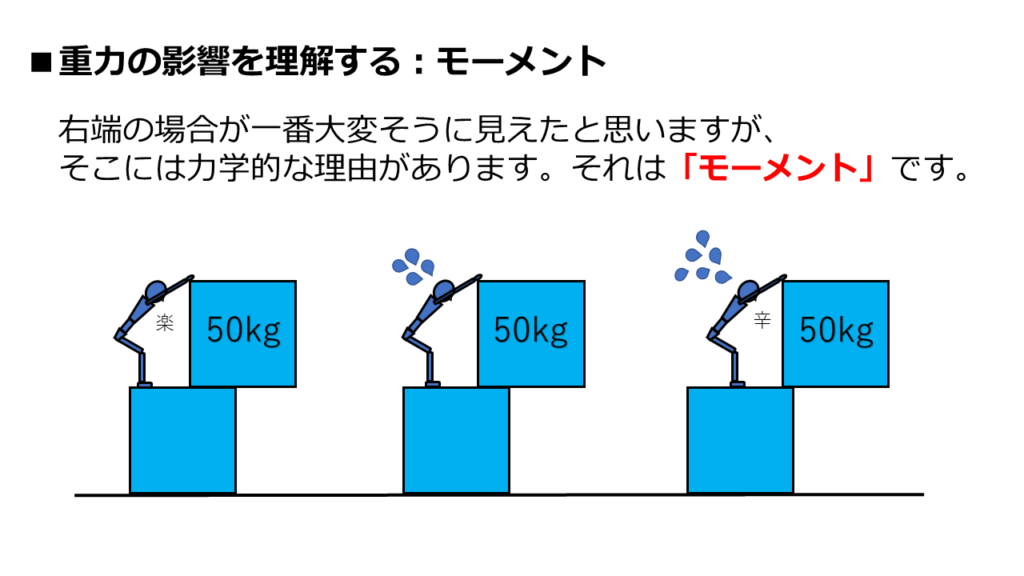
これも、みんな同じ感覚だと思います。
右端が一番大変そうです。
全部同じ50㎏なのに、右端が一番大変そうに見える。
同じ重さを支えているのに、違いが生じるのは何故でしょうか?
その理由は「モーメント」です。
PTなら誰もが聞いたことのある単語ですね。
それと同時に、苦手意識もあるはずです。
でも、その苦手は「思い込み」です。
右端が一番大変そうに見えたなら、あなたは「モーメント」を感覚的には分かっています。
では、その感覚に理屈をつけ足しましょう。

モーメントを簡単に言えば、「てこの原理」で扱われる力のことです。
「支点を軸にして回転しようとする力」のことです。
まずは単純な「てこの原理」で、モーメントを復習します。
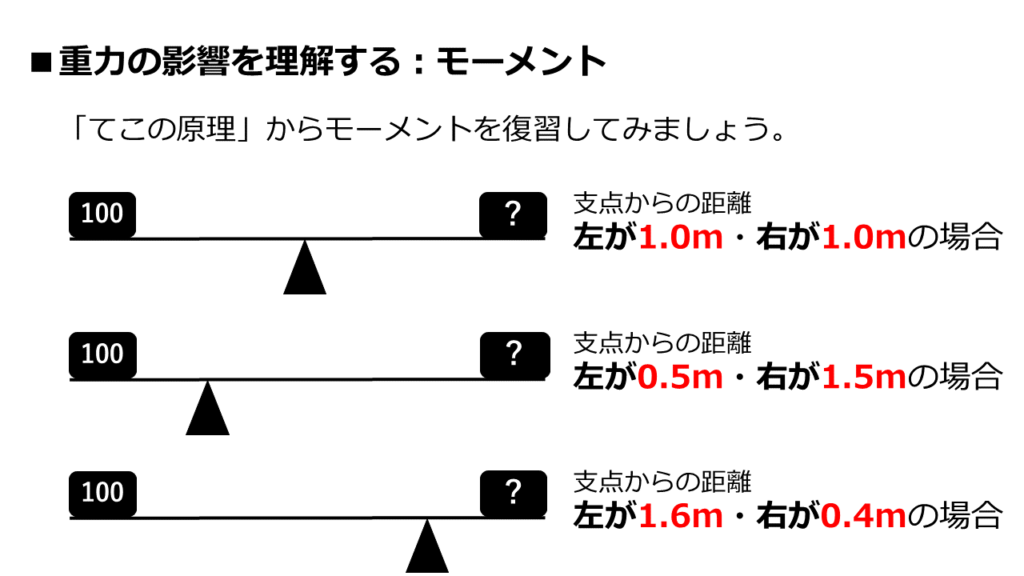
てこのつり合いをとる為に、「?」部分に置かなければならない重さを答えて下さい
1番上は、支点からの距離が1:1
真ん中は、支点からの距離が1:3
1番下は、支点からの距離が4:1
さて、「?」に入る数字はいくつでしょうか?
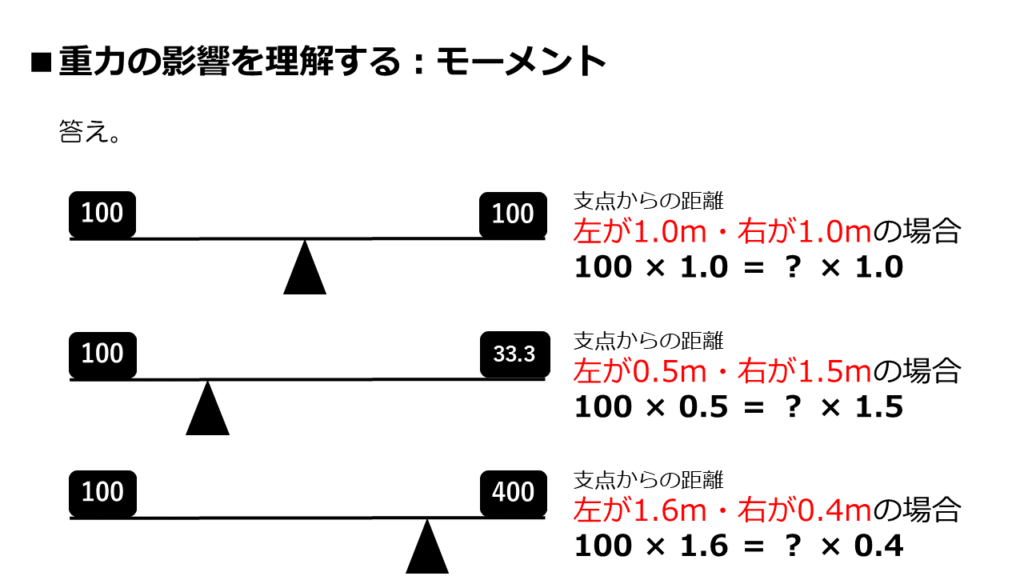
このような式を立てれば、答えは出せますね。
一番上は「100」、真ん中は「33.3」、一番下は「400」が答えです。
厳密に言えば、正しい計算方法ではありませんが、答えが分かればOKです。
支点を軸にして回転しようとする力は、
ざっくり言えば「重さ×支点からの距離」で決まります。
つまり、「支点の左側」と「支点の右側」の計算結果が同じなら、つり合うということです。
そして、一番大事なことは計算方法ではありません。
「支点からの距離が離れるほど、回転しようとする力は増幅する」ということです。
「100と33.3」「100と400」
重さだけで見れば、大きく異なります。
しかし、それでもつり合うのは「支点からの距離」による影響です。
支点からの距離が離れることで、軽い重さでも回転しようとする力が増幅します。
改めての確認ですが、「モーメント」は「支点を軸にして回転しようとする力」です。
「モーメントは支点からの距離が離れるほど増幅する」ということを忘れないで下さい。
では、話を進めていきましょう。
補足として、細かい事をごちゃごちゃ書いていますが、今は読まなくてもいいです。
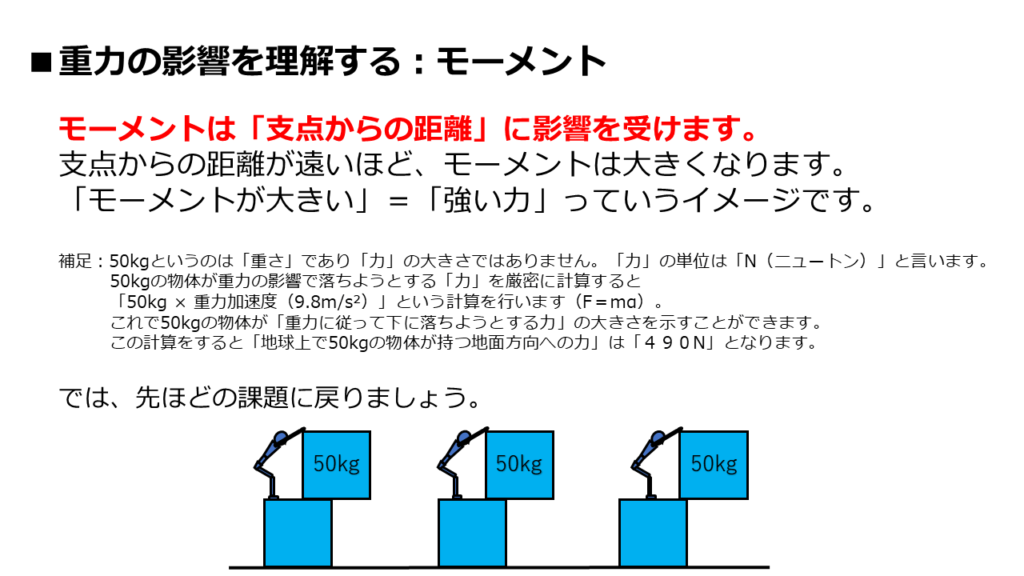
補足説明は、力学に興味を持った時に思い出してください。
今は無視してOKです。
とにかく大事なことは、
「モーメントの大きさ」は「支点からの距離」に影響されるということです。
そして、「モーメントが大きい」=「強い力が発生している」と考えて下さい。
この理屈に基づいて、先ほどの3パターンを振り返ってみましょう。
見た感じの印象は、一番右が大変そうに見えました。
果たして、感覚と理屈は合っているでしょうか?
「モーメント」の理屈で説明していきます。
余計なものを無くして、「てこの原理」で考えやすい形にしていきます。
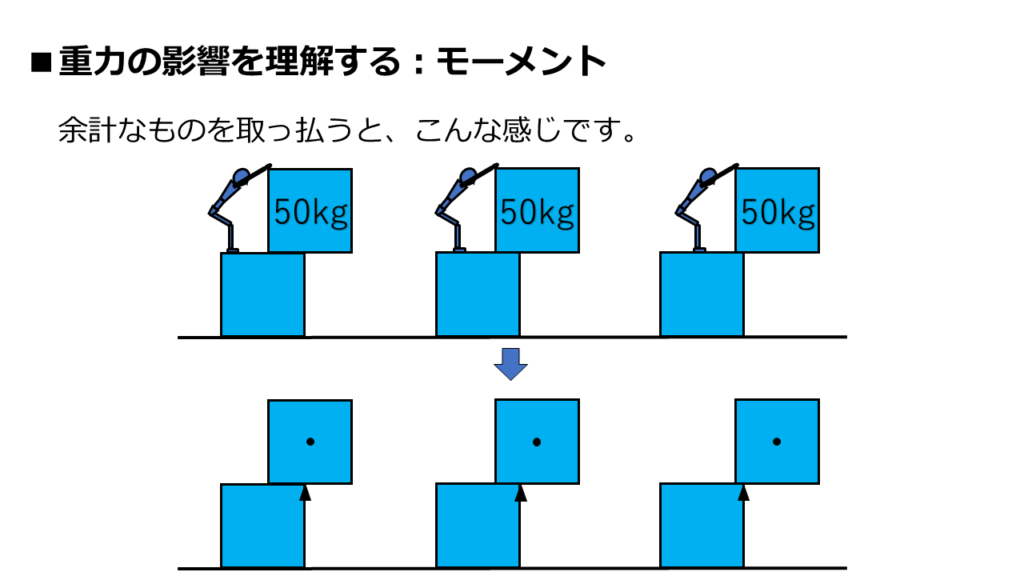
まず、上側の正方形の「重心」を黒丸で示します。
この「重心」に重力が影響してきます。
さらに、「てこの支点」を書き加えます。
黒三角形が「支点」です。
支点の場所は「下側の正方形の端」です。
支持基底面の端とも言えます。
そうなる理由は、「四角形を押さえている手を離したらどうなるか?」で考えます。
もし手を離したら、上側の正方形は、どのように落ちるでしょうか?
感覚的に「時計回りに回転しながら落ちていきそう」に見えませんか?
イメージできますでしょうか?
実際に落ちる時は、時計のように綺麗な回転運動ではありません。
時計回りに回転するような動きは、最初の瞬間だけだと思います。
その後は、回転運動というよりも、傾いた四角形がそのまま落ちていくように見えると思います。
今回想定している「てこの支点」は、手を離した最初の瞬間だけに見られる回転運動で想定しています。
では、てこを完成させていきましょう。
さらに書き加えるのは「力」です。
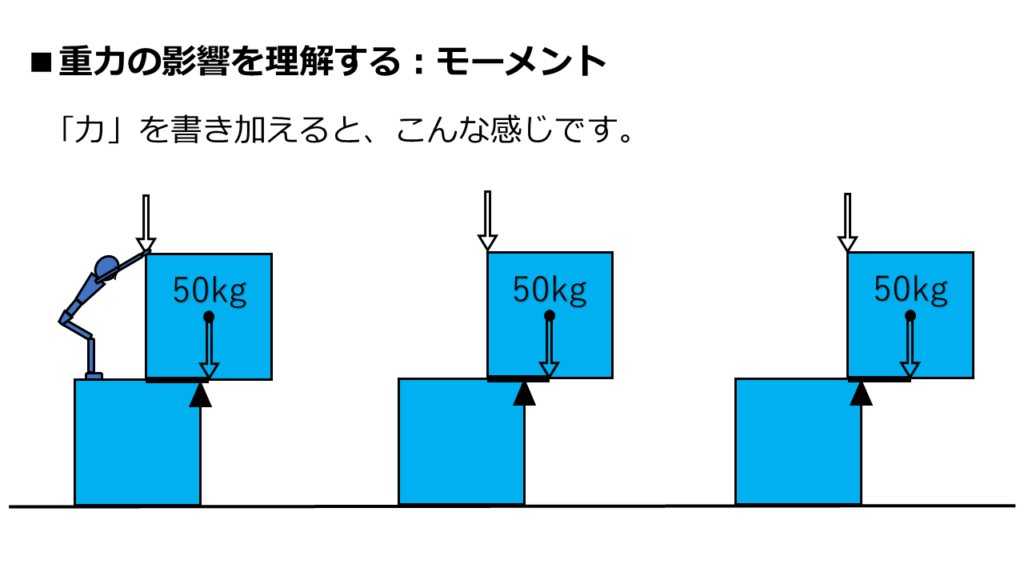
矢印が「力」です。
今回のケースでは、2つの力を書き加えます。
まず1つが「重力の影響で正方形が真下に落ちようとする力」です。
もう1つが「正方形を落とさないように人が支える力」です。
「重力の影響による力」は、正方形の重心から伸びる下向き矢印です。
重力の影響は「常に真下方向」です。
もしも、この重心の真下に「支持基底面」があれば、落ちることはありません。
その場合、なにもしなくても正方形は落ちません。
しかし、今回のように、重心の真下に支持基底面が無ければ正方形は落ちてしまいます。
つまり、50㎏の正方形が落ちないようにするには、何らかの「力」が必要な状況です。
そこで、人が頑張って支えています。
正方形が落ちないように力を加えて、落下を防いでいます。
それが、もう1つの矢印です。
人の手の部分にある下向き矢印が「人が支える力」です。
このように、正方形を上から押さえて、落下を防いでくれています。
この人の頑張りが無ければ、重力の影響によって正方形は落下します。
ここまでの理解は大丈夫そうですか?
要するに、「重力」と「人が支える力」の力比べです。
では、さらに話を進めていきます。
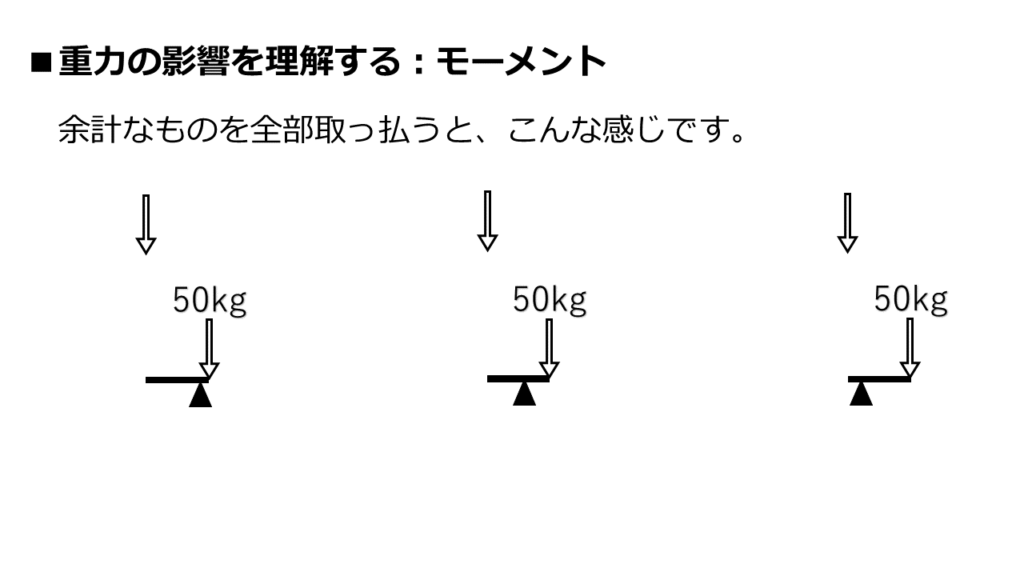
簡略化しました。
正方形も人も消して、「てこ」と「力の矢印」だけが残るようにしました。
イメージしやすくなってきましたね。
もうひと手間加えて、「てこ」を完成させます。
次の工程が最後です。
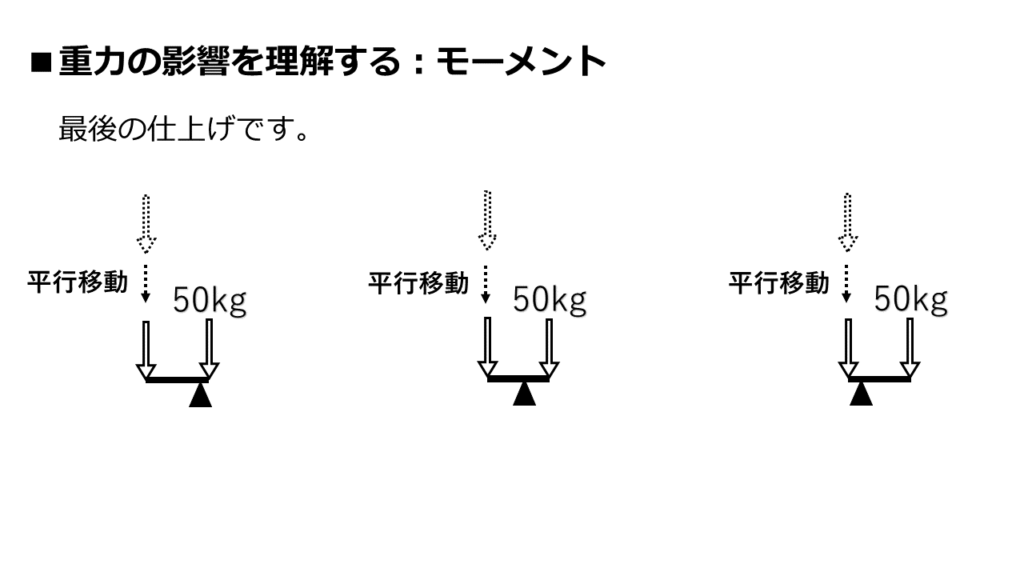
「人が支える力」の矢印を、てこにくっつくように移動しました。
勝手に動かしていいの?という印象もあるかもしれませんが、OKです。
力の矢印は、平行移動なら移動可能だからです。
どこへでも自由に動かしていいわけではありません。
必ず、矢印の向きに合わせた平行移動です。
これで、「てこ」が完成しました。
では改めて、3パターンを比較してみましょう。
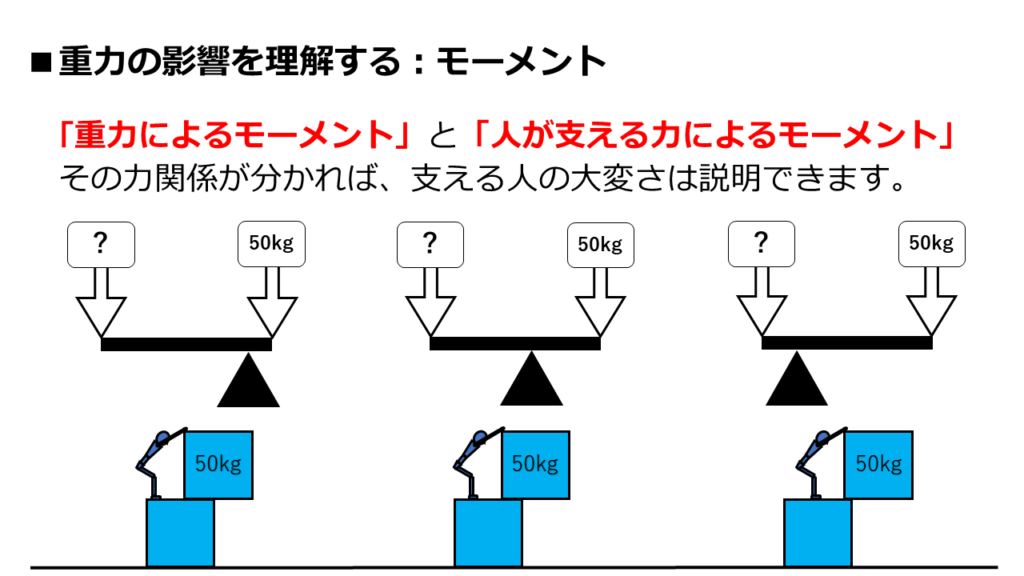
いかがでしょうか?
こんな理屈が隠れていたわけです。
どれも50㎏で重さは一緒なのに、右端の場合が大変そうに見える。
そう感じたのは、「正方形の重心位置」が「てこの支点」から最も離れていたからです。
てこを回転させる力は「モーメント」でしたね。
そして、モーメントは「重さ×距離」です。(厳密には「力×距離」です)
支点からの距離が遠いほど、回転しようとする力は増幅します。
これが原因で、右端の場合は「大きな回転力」が発生していたのです。
1番楽そうに見えた左端のパターンは、
「正方形の重心」と「支点からの距離」が近いです。
逆に、「人による力」と「支点」の距離は離れています。
この位置関係なら、少ない頑張りで支えることが出来ます。
皆さんが感覚的に分かっていたことを、「モーメント」で説明出来ました。
それでは、さらに話を進めていきます。
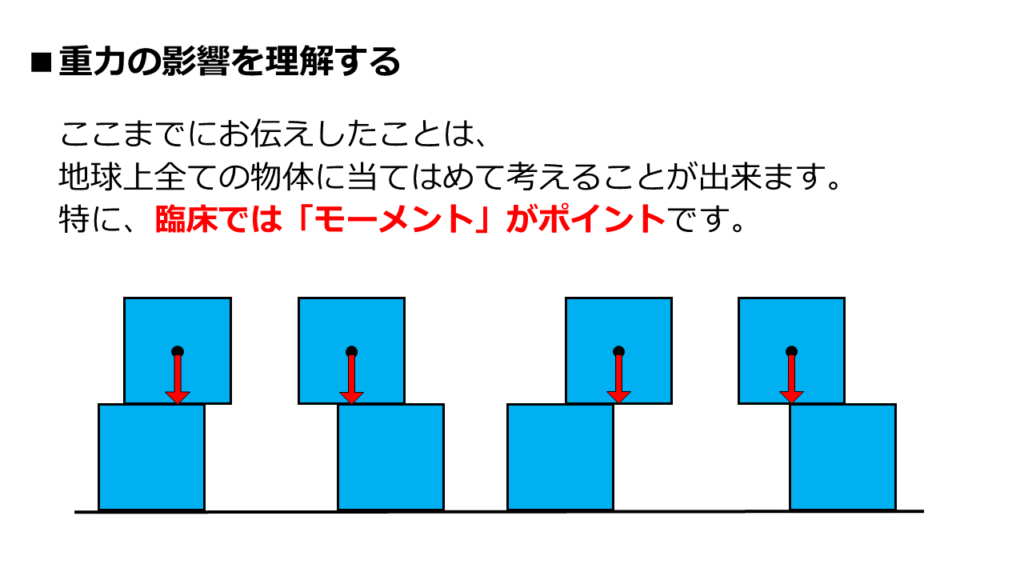
「重心」「重心と支持基底面の関係」「モーメント」
ここまでに説明してきた力学の基礎知識です。
大まかな理解はできましたか?
これらの理屈は、地球上全ての物体に当てはめることが出来ます。
人間も例外ではありません。
もちろん、患者さんも例外ではありません。
あなた自身も、例外ではありません。
地球で生きている人間は、24時間365日、このような理屈の中で生活しています。
全人類に共通する理屈です。
例外はありません。
そして、「共通の理屈」を活用していくことが、安定的な臨床への第一歩です。
では次に、ここまでに確認した基礎知識を、臨床に繋げましょう。
臨床への応用も「モーメント」がポイントです。
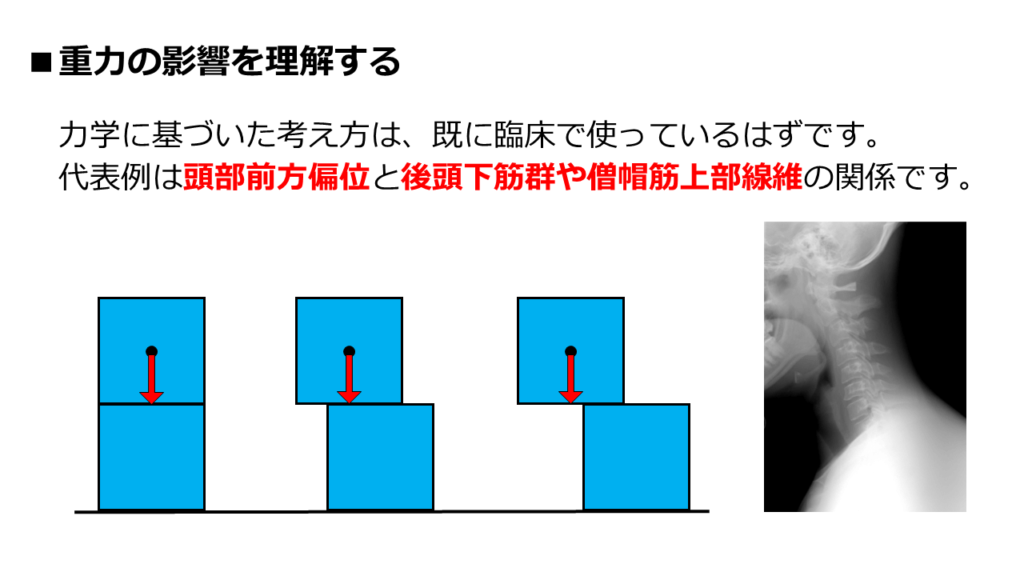
では、力学の基礎知識を臨床に当てはめてみましょう。
とは言っても、既にあなたは、臨床で利用していると思います。
取り上げる例は、「頭部前方偏位による頭頚部の筋への負担」です。
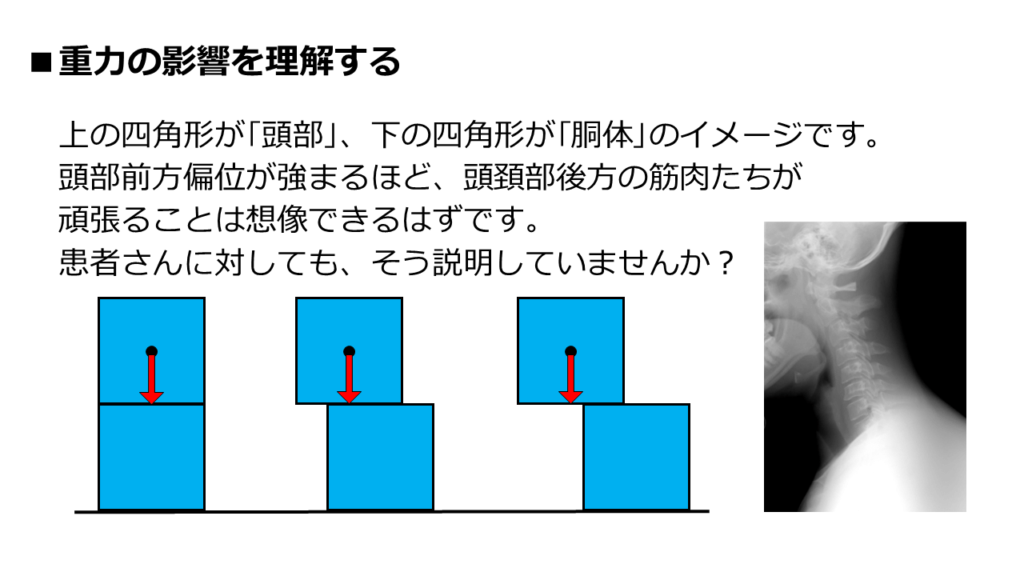
頭部前方偏位による頭頚部後方筋群の筋緊張亢進。
よくあるケースです。
患者さんに対しても、こんな説明をしたことはありませんか?
「姿勢が崩れて首の緊張が強くなってしまっています」
その説明の通り、頭部重心が前方にズレることで筋緊張は亢進します。
頭部の重さは変わりませんが、「頭部重心」と「支点」の距離が離れます。
その結果、頭部が真下に落ちようとする「重力の影響による力」は増幅されます。
すなわち、「モーメント」が大きくなります。
その大きくなったモーメントに抵抗して、
頭部を支え続けなければならないのが、頭頚部後方の筋たちです。
僧帽筋上部線維などは、「頭部が落ちようとする力」とつり合いをとる為に頑張ります。
頭部の位置が大きくズレている姿勢ほど、筋の頑張りは増加します。
このように、人の体に「てこの原理」を応用することは、既に経験があるはずです。
何となくそうしていたかもしれませんが、何となくでは「再現性」がありません。
意図的に、意識的に、力学の基礎知識を活用して下さい。
今回のポイントは、以下のとおりです。

上記のポイントは、しっかりとイメージできるように何度も復習して下さい。
そして、可能な限り、臨床でイメージしてみて下さい。
あなたが担当する患者さんの痛みと、必ず関係しています。
たぶん、最初のうちは難しく感じるはずです。
自分の考え方で正しくやれているのか、疑問を感じることもあると思います。
理屈では理解できても、実践となると難しいはずです。
でも、がんばって続けて下さい。
そして、今後の解説も参考にして下さい。
今後の解説では、より詳細かつ具体的に、臨床での実践方法を解説しています。
それでは次回は「具体的な症例紹介」をします。
力学の基礎知識を、どのように臨床へ応用すればいいのか?
参考にしていただけたらと思います。
ちなみに、取り上げる症例は「頭部前方偏位」です。
頭部前方偏位がもたらす様々な悪影響を、力学にもとづいて解説していきます。
そして、次回の動画をご覧になる前に、
あなたなりに「頭部前方偏位による悪影響」を考えてみて下さい。
「外力」⇒「内力」⇒「組織損傷」⇒「痛み」
この流れを踏まえて、頭部前方偏位がもたらす「痛み」を考察してみて下さい。
次回の動画では、症例を3つ紹介します。
どんな症例となりそうか、ぜひ考えてみて下さい。
それでは、次回もよろしくお願いします。
STEP4の動画はこちら




コメント